
高等数学课件D12数列的极限
25页
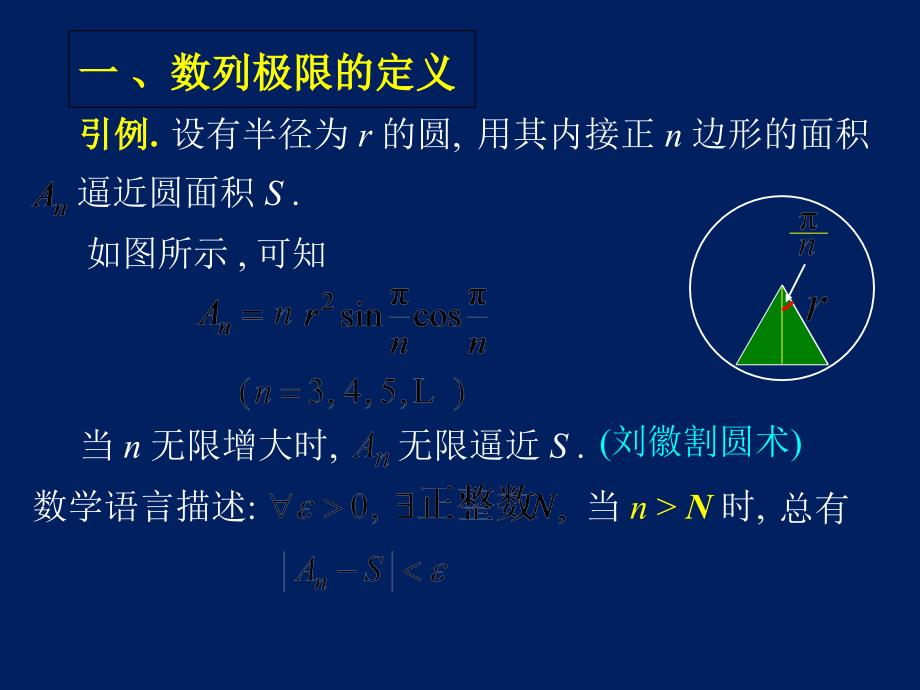

点击阅读更多内容
- 1、金锄头文库是“C2C”交易模式,即卖家上传的文档直接由买家下载,本站只是中间服务平台,本站所有文档下载所得的收益全部归上传人(卖家)所有,作为网络服务商,若您的权利被侵害请及时联系右侧客服;
2、如你看到网页展示的文档有jinchutou.com水印,是因预览和防盗链等技术需要对部份页面进行转换压缩成图而已,我们并不对上传的文档进行任何编辑或修改,文档下载后都不会有jinchutou.com水印标识,下载后原文更清晰;
3、所有的PPT和DOC文档都被视为“模板”,允许上传人保留章节、目录结构的情况下删减部份的内容;下载前须认真查看,确认无误后再购买;
4、文档大部份都是可以预览的,金锄头文库作为内容存储提供商,无法对各卖家所售文档的真实性、完整性、准确性以及专业性等问题提供审核和保证,请慎重购买;
5、文档的总页数、文档格式和文档大小以系统显示为准(内容中显示的页数不一定正确),网站客服只以系统显示的页数、文件格式、文档大小作为仲裁依据;
6、如果您还有什么不清楚的或需要我们协助,可以点击右侧栏的客服。
新上传的文档
最新标签
公安主题党日
部编版四年级第三单元综合性学习课件
机关事务中心2022年全面依法治区工作总结及来年工作安排
入党积极分子自我推荐
世界水日ppt
关于构建更高水平的全民健身公共服务体系的意见
空气单元分析
哈里德课件
2022年乡村振兴驻村工作计划
空气教材分析
五年级下册科学教材分析
退役军人事务局季度工作总结
集装箱房合同
2021年财务报表
2022年继续教育公需课
2022年公需课
2022年日历每月一张
名词性从句在写作中的应用
局域网技术与局域网组建
施工网格
薪资体系
运维实施方案
硫酸安全技术
柔韧训练
既有居住建筑节能改造技术规程
建筑工地疫情防控
大型工程技术风险
磷酸二氢钾
2022年小学三年级语文下册教学总结例文
少儿美术-小花
2022年环保倡议书模板六篇
2022年监理辞职报告精选
2022年畅想未来记叙文精品
企业信息化建设与管理课程实验指导书范本
草房子读后感-第1篇
小数乘整数教学PPT课件人教版五年级数学上册
2022年教师个人工作计划范本-工作计划
国学小名士经典诵读电视大赛观后感诵读经典传承美德
医疗质量管理制度 2
2022年小学体育教师学期工作总结
2022年家长会心得体会集合15篇
农村发展调研报告_1范文
2022年电脑说明文作文合集六篇
2022年防溺水初中生演讲稿
2021最新36岁儿童学习与发展指南心得体会
2022年新生迎新晚会策划书模板
20 xx年教育系统计划生育工作总结
英语定语讲解ppt课件
2021年4s店客服工作计划范文
2022年小学优秀作文700字四篇


